Housing Price Predictions (part 2)

In this post, we will use the Ames housing data to compare several models. The models will be trained to predict sale price and performance will be measured by the root mean squared error (rmse).
We will compare a simple linear regression (lm) with glmnet (lasso and elastic-net regularized generalized linear model), decision trees, random forest and xgboost models. Where appropriate, we will also try to improve model performance with hyperparameter tuning. Let’s get to it!
ames_df <- make_ames() %>%
janitor::clean_names() %>% # extracting the data from the AmesHousing package and converting all column names to lower, snake_case
mutate(sale_price = log10(sale_price))Splitting and creating k-fold cross-validation data
library(rsample)
set.seed(518)
ames_split <- initial_split(ames_df, prop = 0.8, strata = "sale_price") #strata argument will insure that the prediction variable is equally represented in the training and test sets
ames_train <- training(ames_split)
ames_test <- testing(ames_split)
folds <- vfold_cv(ames_train, v = 10, strata = "sale_price")Variable importance
Before we delve into building models, let’s consider which features have the most explanatory power based on the random forest model.
#use vip (variable importance package to predict the importance of our expanatory variables)
rand_forest(mode = "regression") %>%
set_engine("ranger", importance = "impurity") %>%
fit(sale_price ~ .,
data = ames_train) %>%
vip::vip()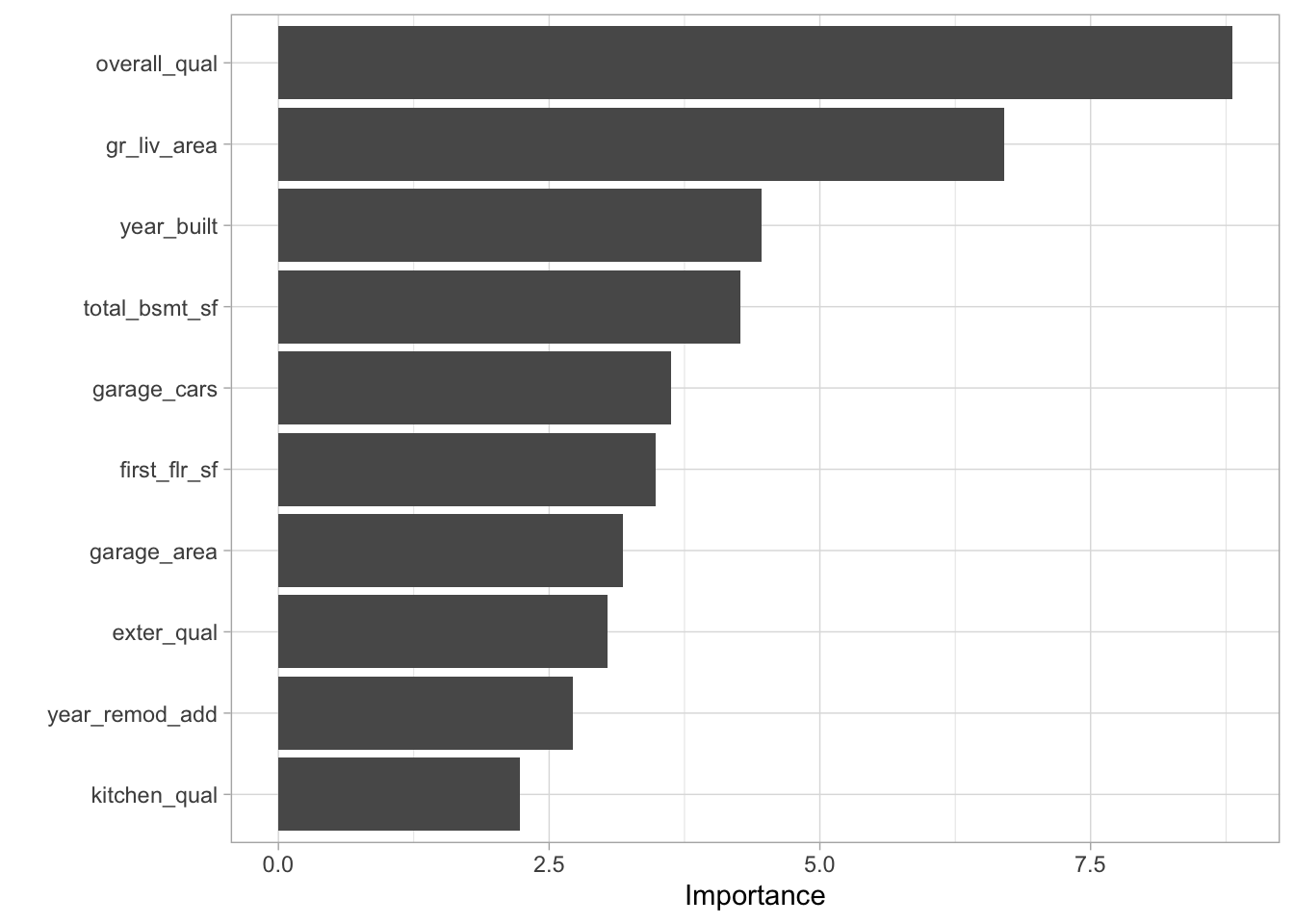
ames_train$overall_cond %>% levels() ## [1] "Very_Poor" "Poor" "Fair" "Below_Average"
## [5] "Average" "Above_Average" "Good" "Very_Good"
## [9] "Excellent" "Very_Excellent"rand_forest(mode = "regression") %>%
set_engine("ranger", importance = "impurity") %>%
fit(sale_price ~ neighborhood + gr_liv_area + year_built + bldg_type,
data = ames_train) %>%
vip::vip()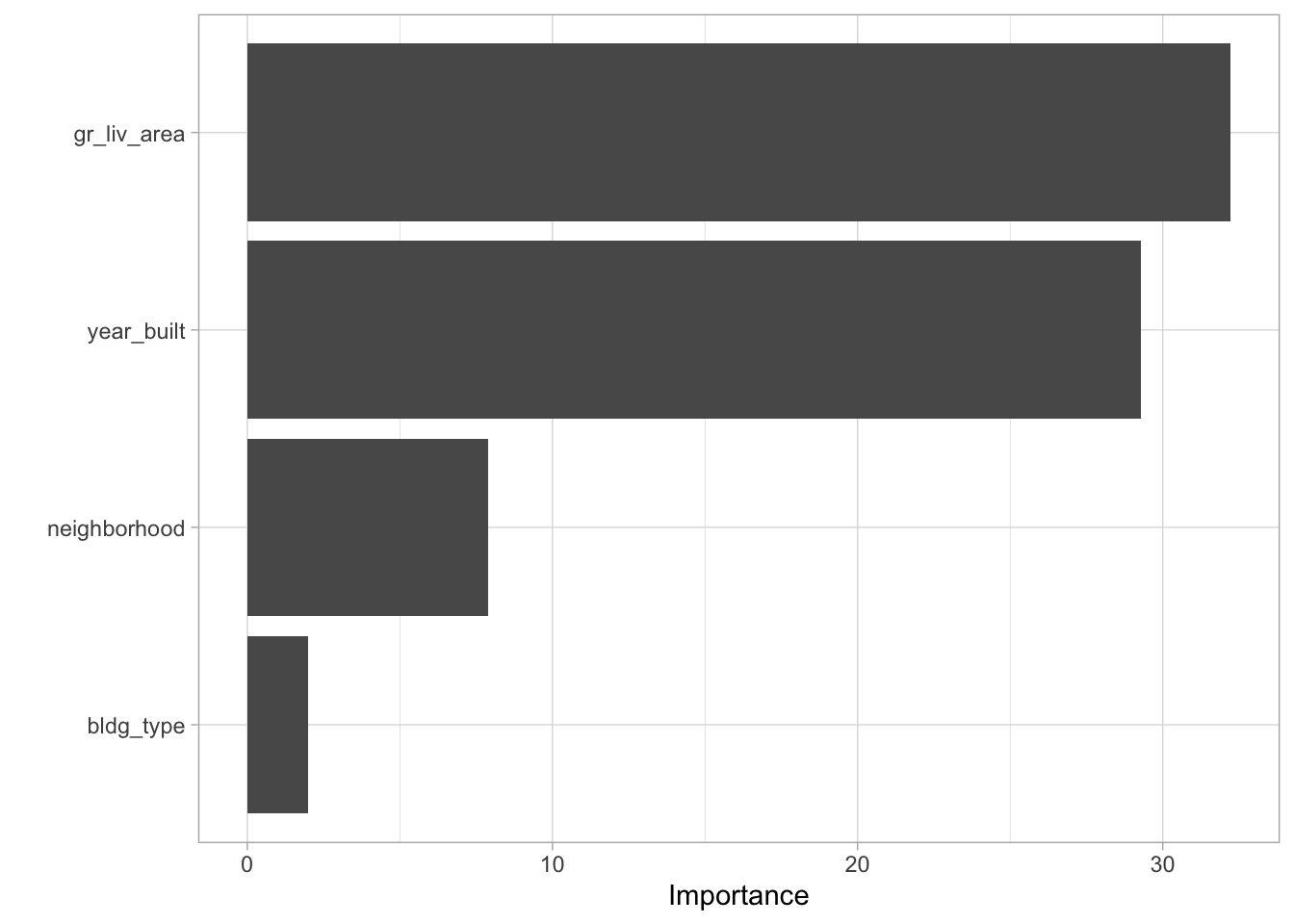
# Let's visualize the relationship between sale price and gr_liv_area.
ggplot(ames_train, aes(x = gr_liv_area, y = sale_price)) +
geom_point(alpha = .2) +
facet_wrap(~ bldg_type) +
geom_smooth(method = lm, formula = y ~ x, se = FALSE, col = "red") +
scale_x_log10() +
scale_y_log10() +
labs(x = "Gross Living Area", y = "Sale Price (USD)")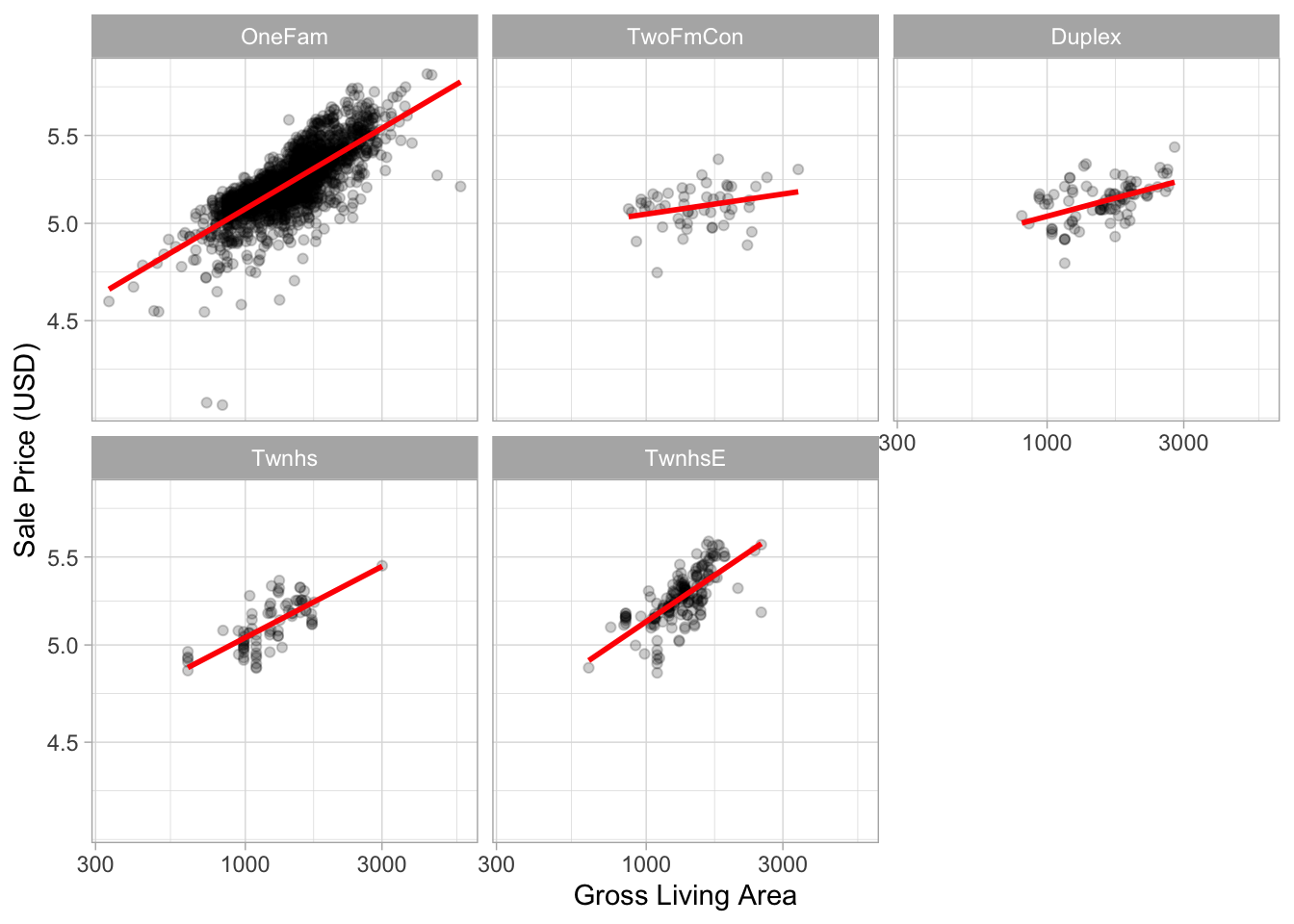
Data preprocessing and formula specification
The feature engineering steps in this post were adapted from Julia Silge and Max Khun’s tidymodels with R textbook.
The formula specification has the form prediction_variable ~ predictor_variables. In this model, the predictor variables include neighborhood, living area, year built and building type.
ames_rec <-
recipe(sale_price ~ overall_cond + gr_liv_area + year_built + bldg_type,
data = ames_train) %>%
step_log(gr_liv_area, base = 10) %>% #log transform gr_liv_area
step_corr(all_numeric(), - all_outcomes()) %>% #remove variables with large correlations
step_nzv(all_predictors()) %>% #remove variables that are highly sparse and unbalanced
#step_other(neighborhood, threshold = 0.01) %>% #pool occurring neighborhoods into an "other" category
step_dummy(all_nominal_predictors()) %>% #converts neighborhoods and building type into a numeric binary model
step_interact( ~ gr_liv_area:starts_with("bldg_type_")) #will create new columns based on interactions between the specified features
ames_rec %>% prep() %>% juice() #view the transformed data## # A tibble: 2,342 x 20
## gr_liv_area year_built sale_price overall_cond_Poor overall_cond_Fair
## <dbl> <int> <dbl> <dbl> <dbl>
## 1 2.95 1961 5.02 0 0
## 2 2.99 1971 4.98 0 0
## 3 3.04 1971 5.02 0 0
## 4 3.03 1977 5.11 0 0
## 5 2.92 1975 5.08 0 0
## 6 2.96 1979 5.00 0 0
## 7 2.88 1984 5.10 0 0
## 8 3.01 1920 4.83 0 0
## 9 3.28 1978 5.05 0 0
## 10 2.95 1967 5.09 0 0
## # … with 2,332 more rows, and 15 more variables:
## # overall_cond_Below_Average <dbl>, overall_cond_Average <dbl>,
## # overall_cond_Above_Average <dbl>, overall_cond_Good <dbl>,
## # overall_cond_Very_Good <dbl>, overall_cond_Excellent <dbl>,
## # overall_cond_Very_Excellent <dbl>, bldg_type_TwoFmCon <dbl>,
## # bldg_type_Duplex <dbl>, bldg_type_Twnhs <dbl>, bldg_type_TwnhsE <dbl>,
## # gr_liv_area_x_bldg_type_TwoFmCon <dbl>,
## # gr_liv_area_x_bldg_type_Duplex <dbl>, gr_liv_area_x_bldg_type_Twnhs <dbl>,
## # gr_liv_area_x_bldg_type_TwnhsE <dbl>Model evaluation
We expect our model to be better than random chance but how do we know? We can generate the value of a dummy (random chance) model by calculating the standard deviation of sale price.
sd(ames_train$sale_price)## [1] 0.1787969# Random chance value: 0.1787969Model 1: linear model
set.seed(212)
ames_lm <- linear_reg() %>%
set_engine("lm")
ames_wkflow <- workflow() %>%
add_model(ames_lm) %>%
add_recipe(ames_rec)
ames_model_train <- ames_wkflow %>%
fit_resamples(resamples = folds,
metrics = metric_set(rmse))
# best_lm <- select_best(ames_model_train)
#
# final_wkflow <- finalize_workflow(ames_wkflow, best_lm)
#
# final_lm_res <- last_fit(final_wkflow, ames_split)
#
# final_lm_res %>% collect_metrics() # rmse: 0.07682275
ames_model_train %>%
collect_metrics(summarize = F) %>%
arrange(.estimate) %>%
filter(.metric == "rmse") %>%
select(rmse = .estimate) %>%
head(1)## # A tibble: 1 x 1
## rmse
## <dbl>
## 1 0.0776# mean rmse for linear model: 0.07974068 Model 2: Glmnet
set.seed(212)
ames_glmnet <- linear_reg(penalty = tune(),
mixture = tune()) %>%
set_engine("glmnet") %>%
set_mode("regression")
ames_glmnet_wkflow <- workflow() %>%
add_model(ames_glmnet) %>%
add_recipe(ames_rec)
glmnet_grid <- grid_random(parameters(ames_glmnet),
size = 7)
glmnet_tunegrid <- ames_glmnet_wkflow %>%
tune_grid(resamples = folds,
grid = glmnet_grid,
metrics = metric_set(rmse),
control = control_grid(save_pred = TRUE))
glmnet_tunegrid %>% collect_metrics()## # A tibble: 7 x 8
## penalty mixture .metric .estimator mean n std_err .config
## <dbl> <dbl> <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 8.45e- 2 0.295 rmse standard 0.111 10 0.00223 Preprocessor1_Model1
## 2 2.81e- 2 0.403 rmse standard 0.0937 10 0.00207 Preprocessor1_Model2
## 3 3.22e- 3 0.452 rmse standard 0.0846 10 0.00166 Preprocessor1_Model3
## 4 1.18e-10 0.486 rmse standard 0.0831 10 0.00169 Preprocessor1_Model4
## 5 5.89e- 9 0.583 rmse standard 0.0831 10 0.00169 Preprocessor1_Model5
## 6 5.34e-10 0.858 rmse standard 0.0831 10 0.00169 Preprocessor1_Model6
## 7 1.13e- 6 0.927 rmse standard 0.0831 10 0.00169 Preprocessor1_Model7autoplot(glmnet_tunegrid)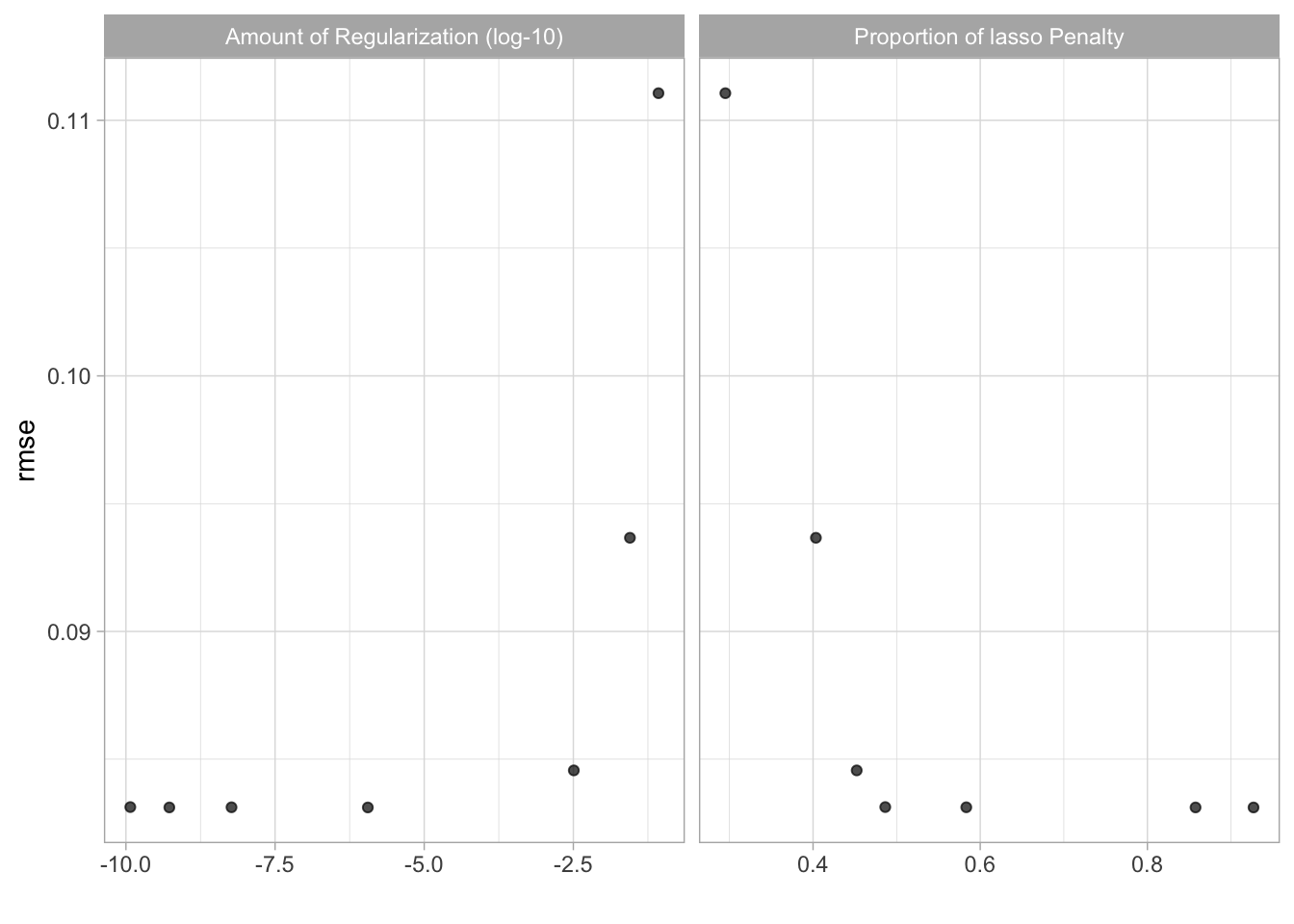
best_rmse <- select_best(glmnet_tunegrid)
final_glmnet <- finalize_workflow(ames_glmnet_wkflow, best_rmse)
final_glmnet %>%
fit(data = ames_train) %>%
pull_workflow_fit() %>%
vip::vip(geom = "point")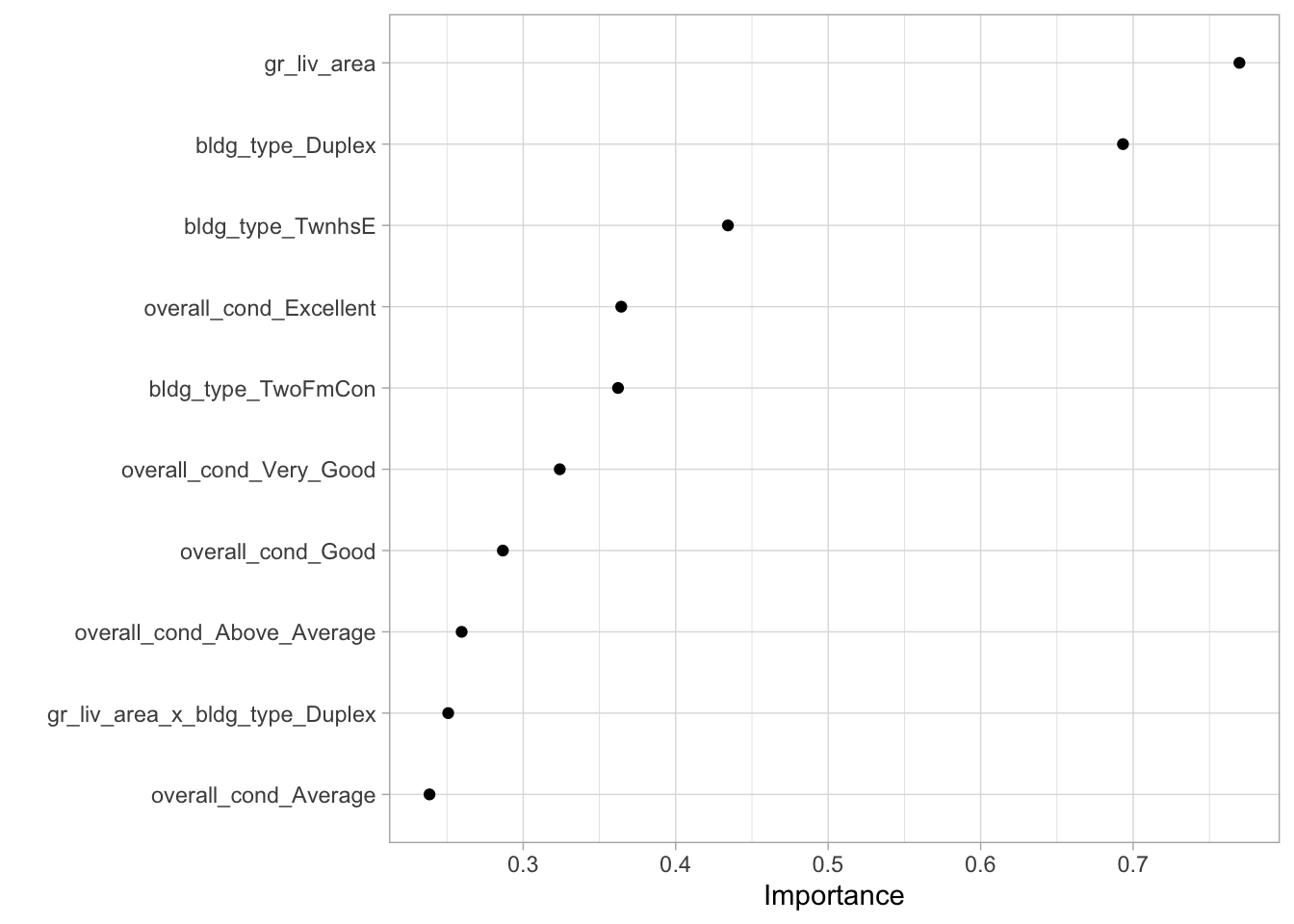
final_glmnet_res <- last_fit(final_glmnet, ames_split)
final_glmnet_res %>%
collect_metrics() # rmse: .0769## # A tibble: 2 x 4
## .metric .estimator .estimate .config
## <chr> <chr> <dbl> <chr>
## 1 rmse standard 0.0822 Preprocessor1_Model1
## 2 rsq standard 0.769 Preprocessor1_Model1Model 3: Decision Tree
ames_decision_tree <- decision_tree() %>%
set_engine("rpart") %>%
set_mode("regression")
decision_tree_wkflow <- workflow() %>%
add_model(ames_decision_tree) %>%
add_recipe(ames_rec)
ames_decision_train <- decision_tree_wkflow %>%
fit_resamples(resamples = folds,
metrics = metric_set(rmse))
show_best(ames_decision_train)## # A tibble: 1 x 6
## .metric .estimator mean n std_err .config
## <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 rmse standard 0.107 10 0.00299 Preprocessor1_Model1ames_decision_train %>%
collect_metrics()## # A tibble: 1 x 6
## .metric .estimator mean n std_err .config
## <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 rmse standard 0.107 10 0.00299 Preprocessor1_Model1best_dec_tree <- select_best(ames_decision_train)
final_dec_tree <- finalize_workflow(decision_tree_wkflow, best_dec_tree)
final_dec_results <- last_fit(final_dec_tree, ames_split)
final_dec_results %>% collect_metrics() # rmse: .09885## # A tibble: 2 x 4
## .metric .estimator .estimate .config
## <chr> <chr> <dbl> <chr>
## 1 rmse standard 0.100 Preprocessor1_Model1
## 2 rsq standard 0.656 Preprocessor1_Model1# mean rmse = 0.1064535Model 4: Random Forest
ames_rand_forest <- rand_forest() %>%
set_engine("ranger") %>%
set_mode("regression")
rf_wkflow <- workflow() %>%
add_model(ames_rand_forest) %>%
add_recipe(ames_rec)
ames_rf_train <- rf_wkflow %>%
fit_resamples(resamples = folds,
metrics = metric_set(rmse))
show_best(ames_rf_train) # rmse = .0825## # A tibble: 1 x 6
## .metric .estimator mean n std_err .config
## <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 rmse standard 0.0880 10 0.00214 Preprocessor1_Model1ames_rf_train %>%
collect_metrics()## # A tibble: 1 x 6
## .metric .estimator mean n std_err .config
## <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 rmse standard 0.0880 10 0.00214 Preprocessor1_Model1# mean rmse = .0823Random Forest with tuning
set.seed(222)
ames_rand_forest_tune <- rand_forest(
trees = 500,
mtry = tune(),
min_n = tune()) %>%
set_engine("ranger") %>%
set_mode("regression")
rf_wkflow <- workflow() %>%
add_model(ames_rand_forest_tune) %>%
add_recipe(ames_rec)
# hypercube_grid <- grid_latin_hypercube(
# min_n(),
# finalize(mtry(), ames_train)
# )
rf_tunegrid <- rf_wkflow %>%
tune_grid(resamples = folds,
#grid = hypercube_grid,
metrics = metric_set(rmse),
control = control_grid(save_pred = TRUE))
rf_tunegrid %>%
collect_metrics() ## # A tibble: 10 x 8
## mtry min_n .metric .estimator mean n std_err .config
## <int> <int> <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 14 32 rmse standard 0.0799 10 0.00222 Preprocessor1_Model01
## 2 9 10 rmse standard 0.0779 10 0.00211 Preprocessor1_Model02
## 3 2 31 rmse standard 0.116 10 0.00208 Preprocessor1_Model03
## 4 13 37 rmse standard 0.0799 10 0.00223 Preprocessor1_Model04
## 5 5 16 rmse standard 0.0829 10 0.00214 Preprocessor1_Model05
## 6 7 28 rmse standard 0.0796 10 0.00222 Preprocessor1_Model06
## 7 5 24 rmse standard 0.0834 10 0.00211 Preprocessor1_Model07
## 8 11 8 rmse standard 0.0788 10 0.00219 Preprocessor1_Model08
## 9 18 20 rmse standard 0.0809 10 0.00209 Preprocessor1_Model09
## 10 17 4 rmse standard 0.0820 10 0.00208 Preprocessor1_Model10rf_tunegrid %>%
collect_predictions()## # A tibble: 23,420 x 7
## id .pred .row mtry min_n sale_price .config
## <chr> <dbl> <int> <int> <int> <dbl> <chr>
## 1 Fold01 5.09 1 14 32 5.02 Preprocessor1_Model01
## 2 Fold01 5.02 22 14 32 5.03 Preprocessor1_Model01
## 3 Fold01 5.09 48 14 32 5.10 Preprocessor1_Model01
## 4 Fold01 5.08 60 14 32 4.95 Preprocessor1_Model01
## 5 Fold01 5.08 63 14 32 5.02 Preprocessor1_Model01
## 6 Fold01 4.79 69 14 32 4.91 Preprocessor1_Model01
## 7 Fold01 4.99 70 14 32 5.04 Preprocessor1_Model01
## 8 Fold01 5.09 85 14 32 5.10 Preprocessor1_Model01
## 9 Fold01 5.00 89 14 32 4.99 Preprocessor1_Model01
## 10 Fold01 5.08 91 14 32 5.08 Preprocessor1_Model01
## # … with 23,410 more rows#mean rmse: 0.07816951Model 5: Xgboost
ames_xgboost <- boost_tree() %>%
set_engine("xgboost") %>%
set_mode("regression")
train_xgboost <- workflow() %>%
add_model(ames_xgboost) %>%
add_recipe(ames_rec) %>%
fit_resamples(resamples = folds,
metrics = metric_set(rmse))
train_xgboost %>%
collect_metrics()## # A tibble: 1 x 6
## .metric .estimator mean n std_err .config
## <chr> <chr> <dbl> <int> <dbl> <chr>
## 1 rmse standard 0.0846 10 0.00191 Preprocessor1_Model1# rmse: 0.08357835Xgboost with tuning
set.seed(123)
# Create the specification with placeholders
boost_spec <- boost_tree(
trees = 500,
learn_rate = tune(),
tree_depth = tune(),
sample_size = tune()) %>%
set_mode("regression") %>%
set_engine("xgboost")
boost_wkflow <- workflow() %>%
add_recipe(ames_rec) %>%
add_model(boost_spec)
# boost_grid <- grid_random(parameters(boost_spec),
# size = 10)
ames_tune <- boost_wkflow %>%
tune_grid(resamples = folds,
#grid = boost_grid,
metrics = metric_set(rmse))
ames_tune %>%
collect_metrics()## # A tibble: 10 x 9
## tree_depth learn_rate sample_size .metric .estimator mean n std_err
## <int> <dbl> <dbl> <chr> <chr> <dbl> <int> <dbl>
## 1 6 2.05e-10 0.765 rmse standard 4.72 10 0.00185
## 2 11 1.25e- 8 0.292 rmse standard 4.72 10 0.00185
## 3 8 6.54e- 3 0.893 rmse standard 0.199 10 0.00166
## 4 9 1.13e- 5 0.926 rmse standard 4.70 10 0.00185
## 5 15 3.00e- 7 0.186 rmse standard 4.72 10 0.00185
## 6 2 1.46e- 4 0.517 rmse standard 4.39 10 0.00186
## 7 12 1.88e- 6 0.641 rmse standard 4.72 10 0.00185
## 8 5 2.88e- 9 0.217 rmse standard 4.72 10 0.00185
## 9 7 3.69e- 2 0.603 rmse standard 0.0799 10 0.00184
## 10 3 3.03e- 4 0.424 rmse standard 4.06 10 0.00188
## # … with 1 more variable: .config <chr>show_best(ames_tune)## # A tibble: 5 x 9
## tree_depth learn_rate sample_size .metric .estimator mean n std_err
## <int> <dbl> <dbl> <chr> <chr> <dbl> <int> <dbl>
## 1 7 0.0369 0.603 rmse standard 0.0799 10 0.00184
## 2 8 0.00654 0.893 rmse standard 0.199 10 0.00166
## 3 3 0.000303 0.424 rmse standard 4.06 10 0.00188
## 4 2 0.000146 0.517 rmse standard 4.39 10 0.00186
## 5 9 0.0000113 0.926 rmse standard 4.70 10 0.00185
## # … with 1 more variable: .config <chr>autoplot(ames_tune)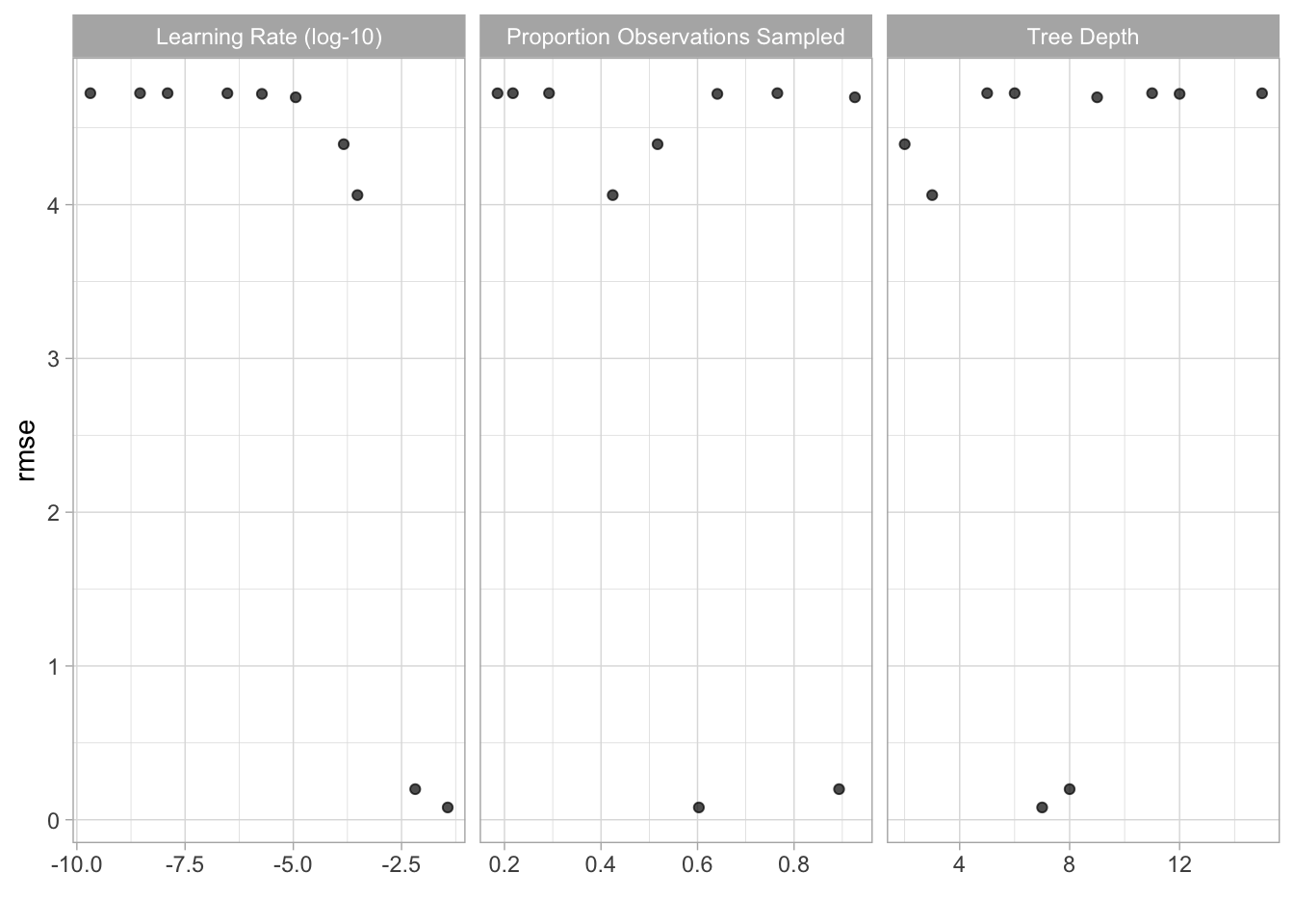
boost_tune_result <- show_best(ames_tune) %>%
select(.metric, mean) %>%
arrange(mean) %>%
filter(row_number() == 1)Results
In this analysis, we compared various regression models and used the tune package to optimize hyperparameter values. The collect_metrics() function allows us to see the possible hyperparameter combinations and the resulting rmse. Let’s compare the rmse values to rank model performance.
library(kableExtra)
model <- c('linear', 'glmnet', 'decision tree', 'random forest', 'random forest tuned', 'xgboost', 'xgboost tuned')
# Function to extract best rmse from each model
extract_rmse <- function(tbl) {
tbl %>%
collect_metrics(summarize = F) %>%
arrange(.estimate) %>%
dplyr::filter(.metric == "rmse") %>%
dplyr::select(rmse = .estimate) %>%
head(1)
}
results = list(ames_model_train, glmnet_tunegrid, ames_decision_train, ames_rf_train, rf_tunegrid, train_xgboost, ames_tune)
model_results <- map_df(results, extract_rmse) %>%
mutate(Model = model) %>%
dplyr::select(Model, rmse) %>%
arrange(rmse)
kable(model_results, caption = "Summary of model performance")| Model | rmse |
|---|---|
| random forest tuned | 0.0708296 |
| xgboost tuned | 0.0714156 |
| xgboost | 0.0749300 |
| glmnet | 0.0770956 |
| linear | 0.0775731 |
| random forest | 0.0814132 |
| decision tree | 0.0937154 |